Atalet Momenti Nedir? Atalet Momenti Hesaplanması

Atalet (Eylemsizlik) Momenti Nedir? Atalet momenti katı cisimlerin, kendi rotasyon hareketlerindeki değişime karşı eylemsizliğinin gösterilmesi durumu olarak bilinmektedir. Hareket etmeyen bir cismin eylemsizliği cismin kütlesi olduğu gibi, dönen bir cismin eylemsizliği de atalet momentidir. Eylemsizlik momenti kavramı iki başlık altında incelenir. Alan eylemsizlik momenti ve kütlesel eylemsizlik momenti:

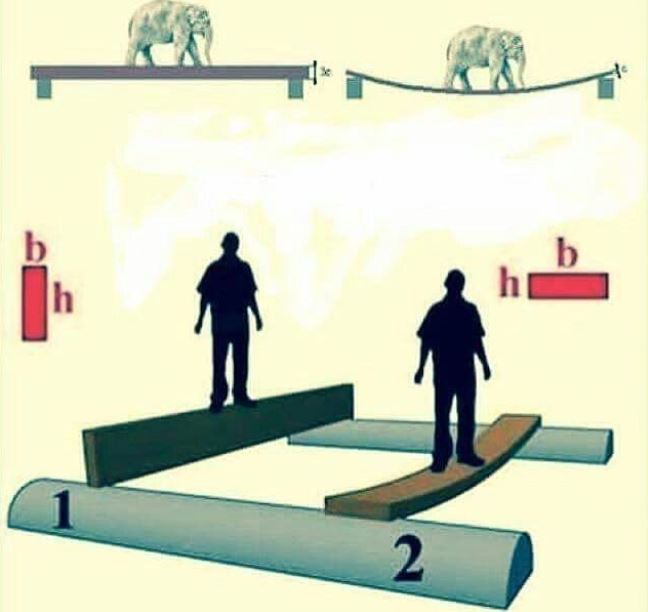
Alan eylemsizlik momenti; Rastgele seçilen bir koordinat sistemine göre bir cismin iki boyutu ele alındığını düşünelim. Bu yüzey, rastgele seçilen koordinat sisteminin bir eksenine dik gelsin. Yüzeyin şekil değiştirmeme isteğinin yüzeyi içine alan eksenlere göre tanımlanmış haline alan atalet momenti ismi verilmiştir. Cismin seçilen yüzeyine dik eksen z ekseni diyelim. İncelenen düzlem x-y düzlemi üzerindedir. Bu şekliyle alan eylemsizlik momenti x eksenine ve y eksenine göre ayrı ayrı tanımlanabilir.

Eylemsizliğin bulunması istenen yüzey homojen ve tek boyutlu ise {\displaystyle \lambda ={\frac {dM}{dL}}={\frac {M}{L}}} $\lambda ={\frac {dM}{dL}}={\frac {M}{L}}$ ; iki boyutlu ise {\displaystyle \sigma ={\frac {dM}{dA}}={\frac {M}{A}}} $\sigma ={\frac {dM}{dA}}={\frac {M}{A}}$ ; üç boyutlu ise {\displaystyle \rho ={\frac {dM}{dV}}={\frac {M}{V}}} $\rho ={\frac {dM}{dV}}={\frac {M}{V}}$ kullanılır.

Atalet Momenti Nedir?

Atalet Momenti Nedir? Atalet Momenti Hesaplanması

$m$ kütleli noktasal bir cisim $r$ uzaklığındaki bir eksen etrafında dönerse bu cismin eylemsizlik momenti $mr^{2}$ olarak tanımlanmaktadır. Cisim çok sayıda parçacıktan oluşmuşsa her bir parçacığın $mr^{2}$ si toplanarak cismin atalet momenti hesaplanmaktadır. Cisim sonsuz küçüklükteki $dm$ kütlelerinden meydana geliyorsa bu cismin atalet momenti
$\int r^{2}dm$ olur.
$L$ boyundaki $M$ kütleli düz bir çubuğun kütle merkezinden geçen eksene göre atalet momenti şöyle hesaplanır:

$dr$ boyundaki küçük bir parçanın kütlesi $dm$ ise $dm={\frac {Mdr}{L}}$
Eksen çubuğun kütle merkezinden geçtiği için integralin sınırları -L/2 ve L/2 olur. Bulduğumuz $dm$ yi formülde yerine alırsak $\int \limits _{-L/2}^{L/2}r^{2}{\frac {Mdr}{L}}$
$M$ ve $L$ sabit olduğundan integralin dışına çıkar, integrali çözersek